Gabeland

Interesting math explorations

recent posts

about

  • Continued Fractions

    This is a continued fraction:

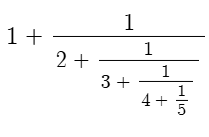
    To evaluate it, just simplify from the bottom up. That one comes out to 225/157.
    For the rest of this, I’m going to use the following notation: 225/157 = [1,2,3,4,5].
    Each number has a unique continued fraction (as long as you don’t use 0), and the rational numbers all eventually terminate.

    But what about irrational numbers? Like, take √2. What’s the continued fraction for that? Well, it ends up being [1, 2, 2, 2, 2, 2, 2, …], with infinite 2s coming after the 1. The notation for this is [1, {2}].
    Why is that √2? Well, let’s consider just [{2}].

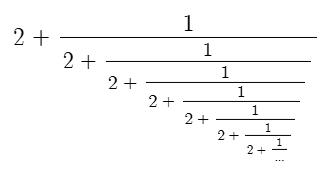
    How would you find the value of this?? The trick is that it contains itself.

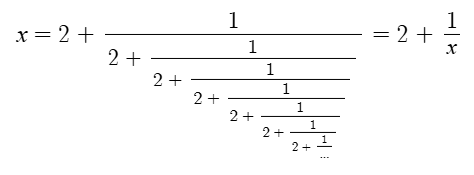
    x = 2 + 1/x means x² – 2x – 1 = 0. That can be easily solved to x = 1 ± √2. Wait, plus or minus? So it could be two different numbers? No. In what world would the value of that be negative?

    Anyways, since that is 1 + √2, we just subtract 1 from it to get the continued fraction of √2.

    Every irrational square root has a repeating continued fraction like that. Here’s the first several of them:
    √2 = [1, {2}]
    √3 = [1, {1, 2}]
    √5 = [2, {4}]
    √6 = [2, {2, 4}]
    √7 = [2, {1, 1, 1, 4}]
    √8 = [2, {1, 4}]
    √10 = [3, {6}]
    √11 = [3, {3, 6}]
    √12 = [3, {2, 6}]
    √13 = [3, {1, 1, 1, 1, 6}]
    √14 = [3, {1, 2, 1, 6}]
    √15 = [3, {1, 6}]
    √17 = [4, {8}]
    √18 = [4, {4, 8}]
    √19 = [4, {2, 1, 3, 1, 2, 8}]
    √20 = [4, {2, 8}]
    Notice any patterns? No? Well, there aren’t a lot of patterns to notice. The first one is that the non-repeating section is always just the next square down. That makes sense. But the repeating section always ends with twice that. And if you ignore the last one, the repeating section is always a palindrome! Why? I don’t know the answer to that myself.

    As well, the square roots that are one above a square have length-1 repeating sections.
    In other words, √(n²+1) = [n, {2n}]. Here’s some other similar patterns I’ve noticed:
    √(n²+2) = [n, {n, 2n}]
    √(n²+4) = [n, {n/2, 2n}] (provided n is even)
    √(n²+n) = [n, {2, 2n}]
    √(n²-2) = [n, {1, n-1, 1, 2n}]
    √(n²-1) = [n-1, {1, 2n-2}]
    But wait, there’s more! The first three are special cases of a more general rule:
    √(n²+k) = [n, {2n/k, 2n}] (of course, this only works if 2n/k is an integer)
    That covers a lot of them, but it still doesn’t explain a lot of things, like why are they all palindromes??

    Let’s move on from square roots for now. What about continued fractions that don’t repeat at all?
    Like this one: [{k}] = [1, 2, 3, 4, 5, 6, 7, 8, …] ≈ 1.43313. I don’t know what that is. (I hope you understand the notation. k starts at 1.)
    There are some that are reasonable values, like e = [2, 1, {2k, 1, 1}]. Or [{2k-1}] = (e²+1)/(e²-1). But most of them are just, who knows.

    How about [{k, 2k}]?

    It’s approximately equal to 1.40848097, and I swear I’ve seen that number before, but I can’t remember from where, and I can’t find it online anywhere. If someone knows a closed form for this number, please let me know.

    Anyways, that was an exploration of continued fractions! I didn’t really know where I was going with it, but I ended up here.

  • Odd Dice

    First week of the new schedule! I already missed it. Anyways, take a basic six-sided die.
    You know, the one that has the numbers from 1 through 6 on it. Roll it twice, and add up the total.
    The result can be anywhere from 2 to 12, but it’s most likely to be 7. You can see this if you look at the number of possibilities for each:

    2 – 11
    3 – 12 21
    4 – 13 22 31
    5 – 14 23 32 41
    6 – 15 24 33 42 51
    7 – 16 25 34 43 52 61
    8 – 26 35 44 53 62
    9 – 36 45 54 63
    10 – 46 55 64
    11 – 56 65
    12 – 66

    What if I told you that there was another set of two dice that had the exact same distribution?
    The first die has the numbers [1,2,2,3,3,4] on it, and the second die has the numbers [1,3,4,5,6,8].
    Let’s just tally the results to check:

    2 – 11
    3 – 21 21
    4 – 13 31 31
    5 – 14 23 23 41
    6 – 15 24 24 33 33
    7 – 16 25 25 34 34 43
    8 – 26 26 35 35 44
    9 – 18 36 36 45
    10 – 28 28 46
    11 – 38 38
    12 – 48

    Yep, it’s the same! But why? Why should these two seemingly arbitrary dice work?

    (d# is a die with that many sides, in case you didn’t know that terminology)
    Well, you can split a d6 into two smaller dice, a d2 and a d3, and add those together. You could have a d2 with [0,1] and a d3 with [1,3,5], or you could have a d2 with [0,3] and a d3 with [1,2,3]. Adding all four of those dice together gives the same result as two d6. So what if we swap them around? Combining the [0,1] with the [1,2,3] makes [1,2,2,3,3,4]. And combining the [0,3] with the [1,3,5] makes [1,3,4,5,6,8].

    But wait, there’s more! What if we combined them in different ways? You could get a d4 with [1,2,4,5] and a d9 with [1,2,3,3,4,5,5,6,7]. (I got this by subtracting one from the d9 sides and adding one to the d4 sides, since that doesn’t change the results.) Or you could have a coin which adds 1 if it’s heads, and a d18 with [2,3,4,4,5,5,6,6,6,7,7,7,8,8,9,9,10,11]. But that last one’s kind of ridiculous, because a d18 doesn’t actually exist. Right?

    There’s also a different way you could look at this: Turn the dice into functions.
    Consider this function: x + x² + x³ + x⁴ + x⁵ + x⁶. The exponents are the possible results, and the coefficients are the number of possibilities for each result.

    If you square it, you get this,
    x² + 2x³ + 3x⁴ + 4x⁵ + 5x⁶ + 6x⁷ + 5x⁸ + 4x⁹ + 3x¹⁰ + 2x¹¹ + x¹²
    which is exactly the distribution for 2 dice.

    However, the important thing about this is that now we can factor them. x + x² + x³ + x⁴ + x⁵ + x⁶ factors into x(x+1)(x²+x+1)(x²-x+1). What is that equivalent to in dice? A d1 with [1], a d2 with [0,1], a d3 with [0,1,2]… and another d1… that has one side with 0, one side with 2… and negative one side with 1? I’ve been trying to come up with a physical interpretation of that for a while, but I think there just is none.

    But, regardless, now we can get the alternate dice a different way.
    The dice need to be six-sided, so the sum of the coefficients has to be 6. How do we find that? Evaluate it at x=1. x+1 evaluates to 2, and x²+x+1 evaluates to 3, so we need those to be paired up. And each one needs an x, otherwise it’d just be equivalent to adding 1 to one of them and subtracting 1 from the other. That leaves only the x²-x+1 term. If we give one of them to each, then you get the original two d6. But if you give them both to one die, and none to the other, then it’s different.

    x(x+1)(x²+x+1) = x + 2x² + 2x³ + x⁴
    x(x+1)(x²+x+1)(x²-x+1)(x²-x+1) = x + x³ + x⁴ + x⁵ + x⁶ + x⁸

    And there you have it! And, furthermore, I’ve now proven that this is the only other way to do it, because there’s no other way to factor x + x² + x³ + x⁴ + x⁵ + x⁶.

  • Circles in circles in circles in…

    I thought of this as a potential math competition problem, but I think it’s better if I share it here!
    Consider the following setup:
    You have a circle of radius 1. Call it O. Two other circles of radius 1/2, A and B, are internally tangent to O and externally tangent to each other, like so:

    Now, C₁ is the circle that is internally tangent to O, but externally tangent to both A and B. There’s actually two of them, so I’ll just pick the top one.

    Next, C₂ is the circle that’s externally tangent to A, B, and C₁. This time there is only one.

    I think you can see where this is going.

    Each successive Cₙ (other than the first) is tangent to A, B, and Cₙ₋₁.
    Now, here’s the question: What is the radius of C₁₀? How would you even figure that out?

    The key to this problem is circular reflection.
    Suppose we’re reflecting across a unit circle. To reflect a point, keep the angle the same but reciprocate the distance from the center, like so:

    An interesting fact about circular reflection is that circles and lines always reflect to other circles and lines. For this, lines are effectively circles that intersect the “point at infinity”, so lines reflect to circles intersecting the center, as that reflects to the “point at infinity”. (1/0 = ∞?)

    Here are some examples:

    How does that help with the problem? Well, let’s reflect it and find out!

    Let’s reflect across O. That seems the most natural.
    With that in mind, what does A map to? It’s tangent to the circle on the left side, so that stays (points on the circle don’t change), and it touches the center, meaning it’s a line. There’s only really 1 possibility for that, then. And B is the same, just on the other side.

    How about C₁? It’s tangent to O, A, and B, so C₁’ should be tangent to O, A’, and B’.

    And C₂ is tangent to C₁, A, and B, so C₂’ is tangent to C₁’, A’, and B’.

    Let’s continue this all the way to C₁₀.

    But how does this help with finding the radius? Well, now we can find the coordinates of the points of tangency.
    The point between O and C₁’ is (0,1). The point between C₁’ and C₂’ is (0,3). The point between C₂’ and C₃’ is (0,5).
    But, go back to the first two. If you go back to the un-reflected version,

    the point between O and C₁ is still (0,1), of course. But the point between C₁ and C₂ is (0,1/3).
    That means the diameter of C₁ is 1-1/3 = 2/3, so the radius is 1/3.
    Likewise, the diameter of C₂ is 1/3-1/5 = 2/15, so the radius is 1/15.
    That gives us exactly what we need to figure out the radius of C₁₀.
    The point between C₉’ and C₁₀’ is (0,19), so the point between C₉ and C₁₀ is (0,1/19).
    And the point between C₁₀’ and C₁₁’ is (0,21), so the point between C₁₀ and C₁₁ is (0,1/21).
    So the diameter is 1/19-1/21 = 2/399, and the radius is 1/399.

    How would anyone ever think of that? They wouldn’t. And that’s why this isn’t actually a math competition question.

    (P.S. I’m starting a schedule. I’ll try to make one post each week, on Saturdays.)

  • Rational Numbers and Infinities

    First, some background.
    The number of natural numbers (1, 2, 3, 4, …) and the number of integers (…, -2, -1, 0, 1, 2, …) are both infinite. But are they the same kind of infinite?
    The answer is yes, because you can match each integer to a natural number.
    Order the integers like this:
    0, 1, -1, 2, -2, 3, -3, 4, -4, …
    and then match each integer to its position.

    But what about rational numbers? You can’t order them that easily. Or can you?
    Well, you can. Let’s look at only the positive ones for the moment; making it both is relatively easy.
    Take a grid of fractions like this:
    1/1 1/2 1/3 1/4 1/5 1/6
    2/1 2/2 2/3 2/4 2/5 2/6
    3/1 3/2 3/3 3/4 3/5 3/6
    etc.
    and take each successive diagonal, so you get the ones where the numerator and denominator add up to 1, then 2, then 3, then 4, etc.
    The order would be 1/1, 1/2, 2/1, 1/3, 2/2, 3/1, 1/4, 2/3, 3/2, 4/1, …
    However, you would get things like 2/2 or 6/3 or 7/14. And the way I’ve always seen that resolved is to just skip over them. If a fraction is the same as one before it, ignore it and move on.

    But that’s unsatisfying.
    Is there a way to order the rational numbers without having to arbitrarily skip things?
    Let’s find out!

    The problem with the previous ordering is that you can have fractions which have a shared factor in the numerator and the denominator. So we need some way to make it so that each factor can only be in the numerator or the denominator, not both.

    Enter the rational prime factorization:
    12/7 = 22 × 31 × 7-1
    This effectively turns every rational number into a finite sequence of integers.
    22 × 31 × 7-1 -> (2, 1, 0, -1)
    It has to be finite, because each positive integer has a greatest prime factor. So after the greatest prime factor of both the numerator and the denominator have passed, there’s no more.

    For the next step, we’re going to want the integers to be converted to positive integers via the ordering at the top. So (2, 1, 0, -1) becomes (4, 2, 1, 3). Keep in mind that adding 1s to the end would make it the same fraction, namely 12/7.
    Now, convert each number to binary. 4 becomes 100, 2 becomes 10, 1 stays 1, and 3 becomes 11.
    Take off the initial 1 (every positive integer has one), and then make all the 0s into 1s and the 1s into 2s.
    Our sequence after that is (11, 1, , 2). The 3rd term is… well, these aren’t exactly numbers. But if you want, you can think of it as 0.

    Lastly, put them together into a ternary number, backwards, separated by 0s.
    12/7 would be 2001011, and converting back into decimal gives us 1489. There we go! We did it!

    …but how do I know we don’t need to skip things? Well, the only opportunity for two of the previous sequences to be the same rational number is if you put 1s on the end of the sequence. But if you put an extra 1 at the end of the sequence, it would put a 0 on the start of the ternary number. And putting a 0 at the start of a number does nothing. In fact, it might as well already be there.

    Here’s part of the list of rational numbers gotten this way:
    1, 2, 1/2, 3, 4, 1/4, 1/3, 8, 1/8, 5, 6, 3/2, 9, 16, 1/16, 1/9, 32, 1/32, 1/5, …
    So, to tie it all together, this shows that the rational numbers and the natural numbers are the same size, because you can pair them and have none left over.

  • Finite Differences

    Let’s say we have a sequence, and we want to guess what polynomial generated it.
    For example:
    3, 10, 19, 30, 43, 58, 75, …
    Finite differences helps with determining that.

    How it works is, take the difference between each pair of terms.
    10 – 3 = 7, then 19 – 10 = 9, then 30 – 19 = 11, etc.
    The new sequence is 7, 9, 11, 13, 15, 17, …
    That’s the odd numbers! Now, which sequence has consecutive pairs of terms differing by odd numbers? The squares. Except this clearly isn’t the squares. So let’s subtract it off:
    3 – 1 = 2
    10 – 4 = 6
    19 – 9 = 10
    etc.
    2, 6, 10, 14, 18, 22, 26, … is the result.
    That’s 4n – 2. So, the function of the original sequence is n² + 4n – 2.

    You can use it for more general cases too.
    Let’s try 8, 33, 88, 185, 336, 553, 848.

    I’m not showing each individual subtraction this time, but here’s the result:
    Step 1: 25, 55, 97, 151, 217, 295
    Step 2: 30, 42, 54, 66, 78
    Step 3: 12, 12, 12, 12

    At step 3, every term is the same. That means that there has to be a cube term, and to find the coefficient, divide the constant term by 3!, or 6. That means there’s a 2n³ term. Let’s subtract that off.
    6, 17, 34, 57, 86, 121, 162

    It still isn’t clear what polynomial this is. But now we can repeat the process with this new sequence.
    Step 1: 11, 17, 23, 29, 35, 41
    Step 2: 6, 6, 6, 6, 6

    Now, every term is the same by step 2. That means there’s a square term, and we can divide the constant term by 2!, which is 2, giving us 3n². Subtract that off again.
    3, 5, 7, 9, 11, 13, 15
    You could do it again, and get a constant term by step 1, but I’m sure you recognize this as 2n + 1.
    So, the full function is 2n³ + 3n² + 2n + 1.

    Finite differences also works for some other functions.
    Take this sequence: 3, 8, 17, 32, 57, 100, 177, …
    Step 1: 5, 9, 15, 25, 43, 77
    Step 2: 4, 6, 10, 18, 34
    Step 3: 2, 4, 8, 16
    That’s the powers of 2. That means that 2ⁿ must be a term in the original function. In fact, the original function was 2ⁿ + n².